Makindo Medical Notes"One small step for man, one large step for Makindo" |
|
|---|---|
| Download all this content in the Apps now Android App and Apple iPhone/Pad App | |
| MEDICAL DISCLAIMER: The contents are under continuing development and improvements and despite all efforts may contain errors of omission or fact. This is not to be used for the assessment, diagnosis, or management of patients. It should not be regarded as medical advice by healthcare workers or laypeople. It is for educational purposes only. Please adhere to your local protocols. Use the BNF for drug information. If you are unwell please seek urgent healthcare advice. If you do not accept this then please do not use the website. Makindo Ltd. |
Physics of flow for Medical students
-
| About | Anaesthetics and Critical Care | Anatomy | Biochemistry | Cardiology | Clinical Cases | CompSci | Crib | Dermatology | Differentials | Drugs | ENT | Electrocardiogram | Embryology | Emergency Medicine | Endocrinology | Ethics | Foundation Doctors | Gastroenterology | General Information | General Practice | Genetics | Geriatric Medicine | Guidelines | Haematology | Hepatology | Immunology | Infectious Diseases | Infographic | Investigations | Lists | Microbiology | Miscellaneous | Nephrology | Neuroanatomy | Neurology | Nutrition | OSCE | Obstetrics Gynaecology | Oncology | Ophthalmology | Oral Medicine and Dentistry | Paediatrics | Palliative | Pathology | Pharmacology | Physiology | Procedures | Psychiatry | Radiology | Respiratory | Resuscitation | Rheumatology | Statistics and Research | Stroke | Surgery | Toxicology | Trauma and Orthopaedics | Twitter | Urology
Related Subjects: |Basic Chemistry for Medicine |Basic Physics for Medicine |Physics of flow for Medical students |Electron Transport Chain |Oxidation and Reduction for Medical Students
Understanding the physics of flow is essential for medical students as it applies to blood circulation, respiratory mechanics, and various medical devices. This guide covers the fundamental principles of fluid dynamics relevant to medicine.
Basic Concepts
- Flow :
- Flow rate is the volume of fluid passing a point per unit time, typically measured in liters per minute (L/min) or milliliters per second (mL/s).
- Types of flow:
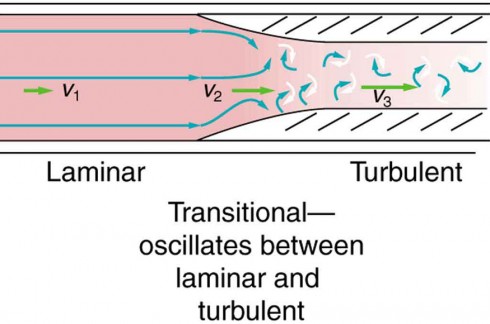
- Laminar Flow : Smooth, orderly flow where fluid moves in parallel layers with minimal mixing. Occurs at low Reynolds numbers.
- Turbulent Flow : Chaotic, irregular flow with eddies and vortices. Occurs at high Reynolds numbers.
Reynolds Number
- Dimensionless number used to predict flow patterns in different fluid flow situations.
- Calculated as: Re = (ρvd)/μ, where:
- ρ = fluid density
- v = flow velocity
- d = characteristic length (e.g., diameter of a blood vessel)
- μ = dynamic viscosity
- Re < 2000 : Laminar flow
- Re > 4000 : Turbulent flow
- 2000 < Re < 4000 : Transitional flow
Poiseuille’s Law
- Describes laminar flow of incompressible fluids through a cylindrical tube.
- Flow rate (Q) is proportional to the fourth power of the radius (r) of the tube and the pressure difference (ΔP), and inversely proportional to the length (L) of the tube and the viscosity (η) of the fluid:
- Q = (πΔPr4) / (8ηL)
- Clinical relevance: Small changes in the radius of blood vessels can significantly affect blood flow.
Bernoulli’s Principle
- Describes the conservation of energy in a flowing fluid.
- As the speed of a fluid increases, its pressure decreases:
- P + ½ρv² + ρgh = constant
- Clinical relevance: Explains phenomena such as the Venturi effect and the behavior of blood flow in narrowed arteries.
Law of Laplace
- Describes the relationship between pressure, radius, and wall tension in cylindrical and spherical structures.
- For a cylinder (e.g., blood vessels):
- T = Pr, where T is wall tension, P is internal pressure, and r is radius.
- For a sphere (e.g., alveoli):
- T = Pr / 2
- Clinical relevance: Important in understanding the mechanics of blood vessels and alveoli, and conditions like aneurysms and respiratory distress syndrome.
Clinical Applications
- Blood Flow :
- Understanding flow dynamics helps in diagnosing and managing conditions like atherosclerosis, aneurysms, and varicose veins.
- Respiratory Mechanics :
- Principles of flow are applied in understanding ventilation, airway resistance, and conditions like asthma and COPD.
- Medical Devices :
- Flow dynamics are essential in the design and function of devices like IV drips, ventilators, and dialysis machines.
Summary
Understanding the physics of flow is crucial for medical professionals to comprehend blood circulation, respiratory mechanics, and the function of various medical devices. Key principles include the types of flow, Reynolds number, Poiseuille’s law, Bernoulli’s principle, and the law of Laplace. Mastery of these concepts aids in diagnosing and treating various medical conditions and improving patient care.